支持向量机(Support Vector Machine, SVM)是一种分类模型,它的基本模型是定义在特征空间上的间隔最大的线性分类器。SVM 还包含核技巧,使它成为非线性分类器。
线性可分支持向量机
先来介绍一些概念。
分割超平面
定义:设 \(C\) 和 \(D\) 为两不相交的凸集,则存在平面 \(P\),\(P\) 可以将 \(C\) 和 \(D\) 完全分离,则 \(P\) 为两集合的分割超平面。
那么如何定义两个集合的“最优”分割超平面?如下图所示,这些线都可以把两个集合完全分开,那么哪条线是最好的?
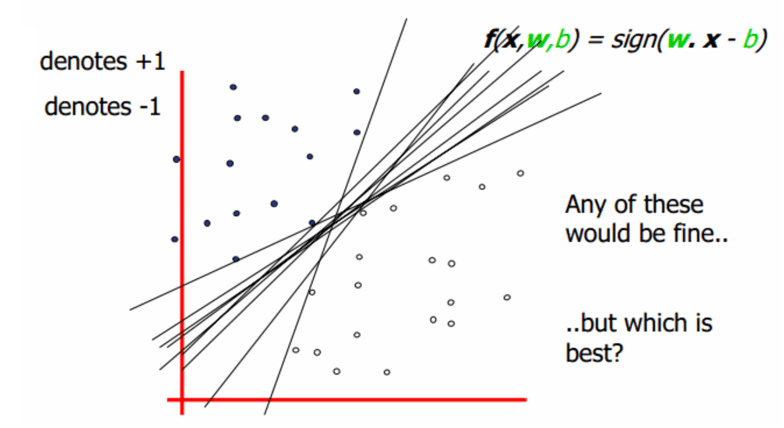
两个集合的距离,定义为两个集合间元素的最短距离。
直观上我们认为如果某一条分割线(或者超平面),使得两个集合到它的最短距离距离最大,那么这条分割线(或超平面)就认为是最优的,因为它最大化地分开了两个集合。
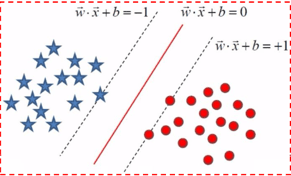
上图红线为最优分割线,平行于它的左右两条虚线为两个集合的边界,过边界的点(向量)起支撑作用,好像把分割超平面支起来一样,所以这些点就叫支撑向量。找到了支撑向量,也就找到了集合边界,也就确定了分割超平面,通过这种方法分类的模型就叫做支持向量机。
硬间隔最大化
输入数据
假设给定一个特征空间上的训练数据集 \[T=\{(x_1,y_1), (x_2,y_2)...(x_N,y_N)\}\] 其中,\(x_i∈R^n\),\(y_i∈\{+1,-1\}\),\(i=1,2,...N\),\(x_i\) 为第 \(i\) 个实例(若 \(n>1\),\(x_i\) 为向量);\(y_i\) 为 \(x_i\) 的类标记。当 \(y_i=+1\) 时,称 \(x_i\) 为正例;当 \(y_i=-1\) 时,称 \(x_i\) 为负例;\((x_i,y_i)\) 称为样本点。
给定线性可分训练数据集,通过间隔最大化得到的分离超平面为 \[y(x) = w^T\Phi(x) + b\]
相应的分类决策函数 \(f(x) = sign(w^T\Phi(x) + b)\) ,该决策函数称为线性可分支持向量机。
\(φ(x)\) 是某个确定的特征空间转换函数,它的作用是将 \(x\) 映射到(更高的)维度。最简单直接的:\(\Phi(x) = x\)。求解分离超平面问题可以等价为求解相应的凸二次规划问题。
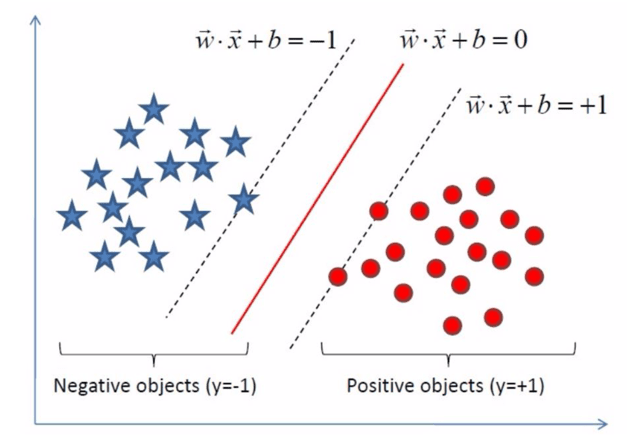
推导目标函数
点到直线距离 平面一点 \(\overrightarrow{x_0}\) 到直线 \(y = \overrightarrow{w}\overrightarrow{x} + b\) 的距离为 \(\frac{|\overrightarrow{w}\overrightarrow{x} + b|}{||\overrightarrow{w}||}\),若直线变换为 \(y = \frac{\overrightarrow{w}\overrightarrow{x} + b}{||\overrightarrow{w}||}\),则距离为 \(|y(\overrightarrow{x_0})|\)
根据题设 \(y(x) = w^T\Phi(x) + b\),有 \(y_i(x)\cdot y(x_i) > 0\),\(w\), \(b\) 等比例缩放,则 \(t*y\) 的值同样缩放,从而样本 \(i\) 到超平面的距离为: \[\frac{y_i\cdot y(x_i)}{||w||} = \frac{y_i \cdot (w^T\Phi(x_i) + b)}{||w||}\]
我们要求最短距离最大的超平面,所以目标函数为:
\[\arg \max_{w, b}\{\frac{1}{||w||}\min_i[y_i \cdot (w^T\cdot \Phi(x_i) + b)]\}\]
由于我们总可以通过等比例缩放 \(w\) 的方法,使得两类点的函数值都满足 \(|y|\geqslant 1\),加上这个约束之后 : \(\min_i[y_i \cdot (w^T\cdot \Phi(x_i) + b)] = 1\),所以目标函数化简为:
\[\arg \max_{w,b}\frac{1}{||w||}\] \[s.t. \ y_i(w^T\cdot \Phi(x_i) + b) \geqslant 1, \ \ i = 1, 2, ... n\]
我们做一下简单的变化,得到:
\[\arg \min_{w,b}\frac{1}{2}||w||^2\] \[s.t. \ y_i(w^T\cdot \Phi(x_i) + b) -1 \geqslant 0, \ \ i = 1, 2, ... n\]
求一个带约束的函数的最值,通常使用Lagrange乘数法。
In mathematical optimization, the method of Lagrange multipliers is a strategy for finding the local maxima and minima of a function subject to equality constraints.
Lagrange函数为:
\[L(w,b,\alpha) = \frac{1}{2}||w||^2- \sum_{i=1}^n\alpha_i(y_i(w^T\cdot \Phi(x_i) + b) - 1)\]
由于我们要求 $_i 0 $,而 \((y_i(w^T\cdot \Phi(x_i) + b) - 1)\) 是一个正值,所以 \(L(w, b, \alpha) \leqslant \frac{1}{2}||w||^2\),即 \(max_\alpha L(w, b, \alpha) = \frac{1}{2}||w||^2\),所以原问题是极小极大问题: \[\min_{w,b}\max_\alpha L(w, b, \alpha)\]
我们再做一下变化,变成原始问题的对偶问题:
\[\max_\alpha\min_{w,b}L(w, b, \alpha)\]
一般情况下,\(\min_y\max_x f(x, y) \geqslant \max_x\min_y f(x, y)\),由于我们的 \(L(w, b, \alpha)\) 满足 KKT条件,所以可以取等号。
由于先求 \(\min_{w,b}\),所以将拉格朗日函数 \(L(w,b,\alpha)\) 分别对 \(w,b\) 求偏导并令其为 \(0\) :
\[\frac{\partial L}{\partial w} = 0 \Rightarrow w = \sum_{i=1}^n\alpha_i y_i \Phi(x_i)\] \[\frac{\partial L}{\partial b} = 0 \Rightarrow \sum_{i=1}^n\alpha_i y_i = 0\]
把上面二式代回 \(L(w, b, \alpha)\),并化简得:
\[\begin{array}{lcl} L(w, b, \alpha) = \frac{1}{2}||w||^2- \sum_{i=1}^n\alpha_i(y_i(w^T\cdot \Phi(x_i) + b) - 1) \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = \frac{1}{2}w^Tw - w^T\sum_{i=1}^n\alpha_iy_i\Phi(x_i) - b\sum_{i=1}^n\alpha_iy_i + \sum_{i=1}^n\alpha_i \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = \frac{1}{2}w^T\sum_{i=1}^n\alpha_i y_i \Phi(x_i) - w^T\sum_{i=1}^n\alpha_iy_i\Phi(x_i) - b \cdot 0 + \sum_{i=1}^n\alpha_i \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = \sum_{i=1}^n\alpha_i - \frac{1}{2}(\sum_{i=1}^n\alpha_i y_i \Phi(x_i))^T\sum_{i=1}^n\alpha_i y_i \Phi(x_i) \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = \sum_{i=1}^n\alpha_i -\frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_j\Phi(x_i)\Phi(x_j) \end{array}\]
继续求 \(\min_{w,b}L(w, b, \alpha)\) 对 \(\alpha\) 的极大:
\[\max_\alpha \sum_{i=1}^n\alpha_i - \frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_j\Phi(x_i)\Phi(x_j)\] \[s.t. \sum_{i=1}^n \alpha_iy_i = 0, \alpha_i \geqslant 0, i = 1, 2, ... n\]
我们对目标函数添加负号,转化为对 \(\alpha\) 求极小:
\[\min_\alpha \frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_j\Phi(x_i)\Phi(x_j) - \sum_{i=1}^n\alpha_i\] \[s.t. \sum_{i=1}^n \alpha_iy_i = 0, \alpha_i \geqslant 0, i = 1, 2, ... n\]
用某些方法(比如:SMO)求得最优解 \(\alpha^*\),然后可以计算出分隔超平面:
\[w^* = \sum_{i=1}^n\alpha_i^*y_i\Phi(x_i)\] \[b^* = y_i - \sum_{i=1}^n\alpha_i^*y_i\Phi(x_i)\cdot \Phi(x_j)\] \[w^*\Phi(x) + b^* = 0\]
其中,\(x_j\) 为某一样本,所以分类决策函数为:
\[f(x) = sign(w^*\Phi(x) + b^*)\]
线性支持向量机
解决问题之后我们发现,有时候不一定分类完全正确的超平面就是最好的,容忍些小错误可能会更好,如下图所示:
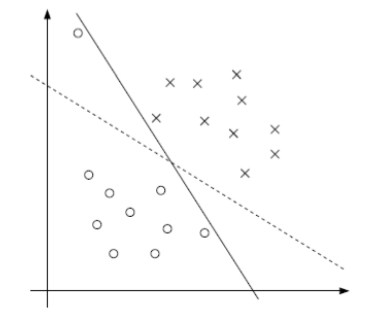
明显虚线比完全分对的实线看起来要好一些,实线可能过拟合了。而且更多的情况是数据集本身就不是线性可分的,解决这些问题就需要用软间隔最大化的线性支持向量机了!
软间隔最大化
若数据线性不可分,则增加松弛因子 \(ξ_i≥0\) , 使函数间隔加上松弛变量大于等于 \(1\)。这样, 约束条件变成 : \[y_i(w\cdot x_i + b) \geqslant 1 - \xi_i\]
则目标函数变为:
\[\min_{w,b, \xi}\frac{1}{2}||w||^2 + C\sum_{i=1}^n\xi_i\] \[s.t. y_i(w\cdot x_i + b) \geqslant 1 - \xi_i, \ \xi_i \geqslant 0, \ i = 1,2, ... n\]
其中,参数 \(C\) 用于调节容忍错误的程度。当 \(C \rightarrow +\infty\) 时,要最小化目标函数,\(\xi_i\) 只能取非常非常小的值,即 \(\xi_i \rightarrow 0\),相当于线性可分SVM;当 \(C\) 比较小时,\(\xi_i\) 可以取得较大的值,从而容错率较大,可防止过拟合。
构造Lagrange函数: \[L(w, b, \xi, \alpha, \mu) = \frac{1}{2}||w||^2 + C\sum_{i=1}^n\xi_i -\sum_{i=1}^n\alpha_i(y_i(w^T\cdot \Phi(x_i) + b) - 1 + \xi_i) - \sum_{i=1}^n\mu_i\xi_i\]
对 \(w, b, \xi\) 求偏导并令其等于 \(0\) 得:
\[\frac{\partial L}{\partial w} = 0 \Rightarrow \sum_{i=1}^n\alpha_iy_i\Phi(x_i)\] \[\frac{\partial L}{\partial b} = 0 \Rightarrow \sum_{i=1}^n\alpha_i y_i = 0\] \[\frac{\partial L}{\partial \xi} = 0 \Rightarrow C - \alpha_i - \mu_i = 0\]
将上面三式代入Lagrange函数得:
\[\min_{w,b,\xi}L(w,b,\xi,\alpha,\mu) = -\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n\alpha_i\alpha_jy_iy_j(\Phi(x_i)\cdot \Phi(x_j)) + \sum_{i=1}^n\alpha_i\]
对上式求关于 \(\alpha\) 的极大,得到:
\[\max_\alpha -\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n\alpha_i\alpha_jy_iy_j(\Phi(x_i)\cdot \Phi(x_j)) + \sum_{i=1}^n\alpha_i\] \[s.t. \sum_{i=0}^n\alpha_iy_i = 0, \ C - \alpha_i - \mu_i = 0, \ \alpha_i \geqslant 0, \mu_i \geqslant 0, i = 1,2...n\]
由于 \(C - \alpha_i - \mu_i = 0\),我们可以知道:\(0 \leqslant \alpha_i \leqslant C\)。
整理得到对偶问题:
\[\min_\alpha \sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n\alpha_i\alpha_jy_iy_j(\Phi(x_i)\cdot \Phi(x_j))\] \[s.t. \sum_{i=0}^n\alpha_iy_i = 0, \ 0 \leqslant \alpha_i \leqslant C,\ i = 1,2...n\]
通过某些方法(比如:SMO)求解约束最优化问题,求得最优解 \(\alpha^*\)。
计算 \(w^*\) 和 \(b^*\) :
\[w^* = \sum_{i=1}^n\alpha_i^*y_i\Phi(x_i)\] \[b^* = \frac{\max_{i:y_i = -1}w^*\Phi(x_i)+\min_{i:y_i = 1}w^*\Phi(x_i)}{2}\]
注意: * 计算 \(b^*\)时,需要使用满足条件 \(0<α_j<C\) 的向量 * 实践中往往取支持向量的所有值取平均,作为 \(b^*\)
求得分离超平面:\(w^*\Phi(x) + b^* = 0\)
分类决策函数为:
\[f(x) = sign(w^*\Phi(x) + b^*)\]
损失函数分析
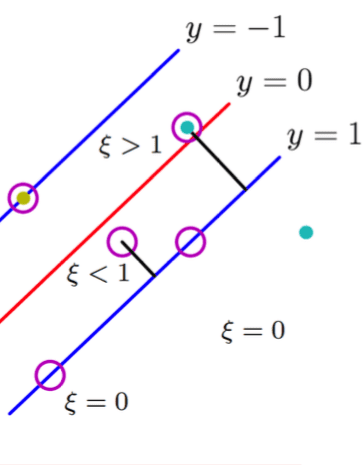
若一正例样本落在 \(y=1\) 下侧或正好在线上,则惩罚 \(\xi = 0\) ;若落在 \(y=0\) 与 \(y=1\) 之间,则惩罚为一个小于 \(1\) 的数,即 \(\xi < 1\);若正好落在分割线上,则 \(\xi = 1\) ;若该样本落在 \(y = 0\) 上侧,则惩罚为大于 \(1\) 的值,即 \(\xi > 1\)。画在坐标轴上就是:
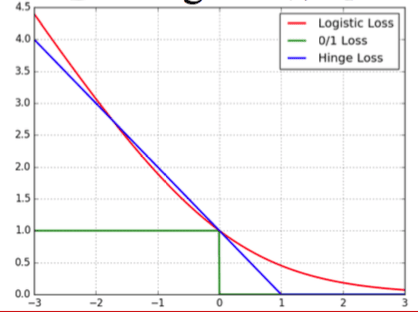
其中,蓝色的线就是SVM的损失函数,红色的线是Logistic回归的损失函数,绿色的线是0/1损失。
非线性支持向量机
可以使用核函数,将原始输入空间映射到新的特征空间,从而,使得原本线性不可分的 样本可能在核空间可分,从而实现非线性支持向量机。
核函数
我们要优化的目标函数为: \[\min_\alpha \sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n\alpha_i\alpha_jy_iy_j(\Phi(x_i)\cdot \Phi(x_j))\]
我们定义核函数 \(\kappa(x_i, x_j) = \Phi(x_i) \cdot \Phi(x_j)\),来代替 \(\Phi(x_i)\) 与 \(\Phi(x_j)\) 的点积,从而我们不用自己提取 \(x\) 的特征 \(\Phi(x)\),只需定义一个核函数来表示两个样本的相似度。
常用的核函数有以下几个: * 多项式核函数:\(\kappa(x_1, x_2) = (\alpha \cdot ||x_1 - x_2||^a + r)^b\),\(\alpha, a, b, r\) 为常数 * 高斯核函数RBF:\(\kappa(x_1,x_2) = \exp(-\frac{||x_1 - x_2||^2}{2\sigma^2})\) * Sigmoid核:\(\kappa(x_1,x_2) = \tanh(\gamma\cdot||x_1-x_2||^a+r)\),\(\gamma,a,r\) 为常数
在实际应用中,往往依赖先验领域知识/交叉验证等方案才能选择有效的核函数;若没有更多先验信息,则使用高斯核函数。
核函数映射
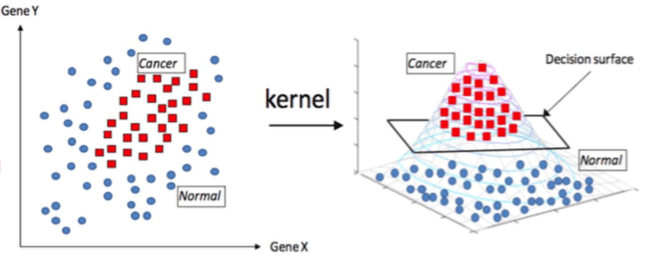
高斯核函数其实可以在样本周围形成一圈圈等高线,使正样本上升形成山峰,负样本下降形成山谷,然后总会有一个或多个超平面可以完美分割两类样本,如上图所示。
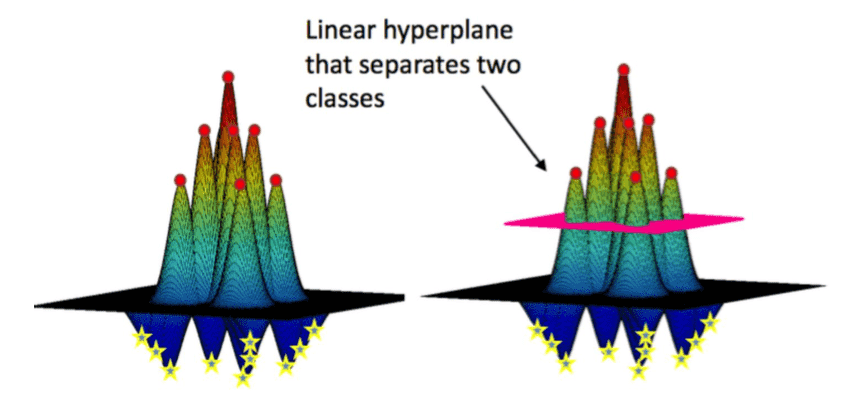
那么多个完美分割的超平面哪个是最好的呢?是粉红色的还是黑色的?
其实我们只需要把样本到平面的最短距离求出来,然后最大化这个距离就可以,没错,就是在核函数映射的空间里做SVM!而且总是可以找到一个最优的分割平面来分割数据集,这也就是 SVM + kernel trick 异常强大的原因。
RBF
在多说一点高斯核函数,\(\kappa(x_1,x_2) = \exp(-\frac{||x_1 - x_2||^2}{2\sigma^2})\)。
\(e^x\) 的Taylor展开:\(e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + ... + \frac{x^n}{n!} + R_n\)
我们对高斯核函数做一些变换并Taylor展开:
\[\begin{array}{lcl} \kappa(x_1,x_2) = e^{-\frac{||x_1 - x_2||^2}{2\sigma^2}} = e^{-\frac{(x_1 - x_2)^2}{2\sigma^2}} \\ \ \ \ \ \ \ \ \ \ \ \ \ \ = e^{-\frac{x_1^2 - 2x_1x_2 + x_2^2}{2\sigma^2}} \\ \ \ \ \ \ \ \ \ \ \ \ \ \ = e^{-\frac{x_1^2 + x_2^2}{2\sigma^2}} \cdot e^{\frac{x_1x_2}{\sigma^2}} \\ \ \ \ \ \ \ \ \ \ \ \ \ \ = e^{-\frac{x_1^2 + x_2^2}{2\sigma^2}} \cdot(1 + \frac{1}{\sigma^2}\cdot\frac{x_1x_2}{1!} + (\frac{1}{\sigma^2})^2\cdot\frac{(x_1x_2)^2}{2!} + ... + (\frac{1}{\sigma^2})^n\cdot\frac{(x_1x_2)^n}{n!} + ...) \\ \ \ \ \ \ \ \ \ \ \ \ \ \ = e^{-\frac{x_1^2 + x_2^2}{2\sigma^2}} \cdot (1\cdot1 + \frac{1}{1!}\frac{x_1}{\sigma}\frac{x_2}{\sigma} + \frac{1}{2!}\frac{x_1^2}{\sigma^2}\frac{x_2^2}{\sigma^2} + ... + \frac{1}{n!}\frac{x_1^n}{\sigma^n}\frac{x_2^n}{\sigma^n}+...) \\ \ \ \ \ \ \ \ \ \ \ \ \ \ = \Phi(x_1)^T\cdot\Phi(x_2) \end{array}\]
其中,\(\Phi(x) = e^{-\frac{x^2}{2\sigma^2}}(1+\sqrt{\frac{1}{1!}}\frac{x}{\sigma} + \sqrt{\frac{1}{2!}}\frac{x^2}{\sigma^2} + ...+\sqrt{\frac{1}{n!}}\frac{x^n}{\sigma^n} + ...)\)
由 \(\Phi(x)\) 结果可见高斯核函数实际把特征映射到了无穷维,然后由SVM选出几个最优维度进行分类。
SMO
SVM中系数的求解:Sequential Minimal Optimization
算法思想 * 有多个拉格朗日乘子 * 每次只选择其中两个乘子做优化,其他因子认为是常数 * 将N个解问题,转换成两个变量的求解问题:并且目标函数是凸的
算法步骤 * 考察目标函数,假设 \(α_1\) 和 \(α_2\) 是变量,其他是定值: \[\min_\alpha \sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n\alpha_i\alpha_jy_iy_j\kappa(x_i,x_j)\] \[s.t. \sum_{i=0}^n\alpha_iy_i = 0, \ 0 \leqslant \alpha_i \leqslant C,\ i = 1,2...n\] * 二变量优化问题 \[y_1 \neq y_2,\begin{cases} L = \max\{0, \alpha_1 - \alpha2\} \\ H = \min\{C, C+\alpha_1-\alpha_2\} \end{cases}\] \[y_1 = y_2,\begin{cases} L = \max\{0, \alpha_1 + \alpha2 - C\} \\ H = \min\{C, \alpha_1+\alpha_2\} \end{cases}\] * 迭代公式 \[g(x) = \sum_{i=1}^ny_i\alpha_i\kappa(x_i, x) + b\] \[\eta = \kappa(x_1, x_1) + \kappa(x_2, x_2) - 2\kappa(x_1, x_2) = ||\Phi(x_1) - \Phi(x_2)||^2\] \[E_i = g(x_i) - y_i = (\sum_{j=1}^ny_j\alpha_j\kappa(x_j, x_i) + b) - y_i,\ \ \ i = 1, 2\] \[\alpha_j^{new} = \alpha_j^{old} + \frac{y_j(E_i - E_j)}{\eta}\] * 迭代 \(m\) 次 \(\alpha_j\) 没有变化就可以退出迭代了,\(m\) 为自己设置的阈值。
总结思考
- SVM可以用来划分多类别吗?
- 答案是肯定的。
- 直接多分类
- 1 vs all
- SVM和Logistic回归的比较
- 经典的SVM,直接输出类别,不给出后验概率
- Logistic回归,会给出属于哪个类别的后验概率
- 二者目标函数的异同
- SVM也可以用于回归问题:SVR
参考文献
- 李航,统计学习方法,清华大学出版社,2012
- Charlie Frogner. Support Vector Machines. 2011
- Corinana Cortes, Vladimir Vapnik. Support-Vector Networks. Machine Learning, 20, 273-297, 1995
- John C. Platt. Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines. 1998
- Andrew W. Moore. Support Vector Machines, 2001